Discover Stellargram Puzzles
Prepare to be captivated by Stellargram, the mesmerising puzzle game that's igniting minds across the globe!
Imagine the challenge of Sudoku, now reimagined in a stunning hexagonal design that's as visually appealing as it is mentally stimulating. Stellargram transforms the classic number-placement puzzle into a cosmic experience.
With its intuitive rules and infinite possibilities, Stellargram offers:
- A fresh twist on familiar logic puzzles
- Gorgeous geometric layouts that please the eye
- Scalable difficulty to challenge novices and experts alike
- A perfect blend of relaxation and mental exercise
Whether you're a seasoned puzzle solver or new to the world of logic games, Stellargram invites you to explore its galaxy of brain-teasing challenges. Get ready to embark on a journey of discovery – your next obsession awaits in the stars of Stellargram!
Availability: Daily
Rules:
Use numbers 1-6 only.
Fill the spaces around each circle core with numbers 1-6.
No number can repeat in any partial hexagon along the puzzle's border.
Tips for Solving:
Look for overlapping spaces between hexagons. These must contain the same number for all connected hexagons.
Identify spaces that can only contain one specific number due to the numbers already present in adjacent hexagons.
Remember, patience and logical thinking are key to mastering Stellargram!
Detailed Instructions
A Stellargram is composed of hexagons and numbers from 1 to 6 are used. There are two rules to respect:
Put the numbers from 1 to 6 in each 13 hexagon, each hexagon has a circle in centre.
1.
2.
3.
4.
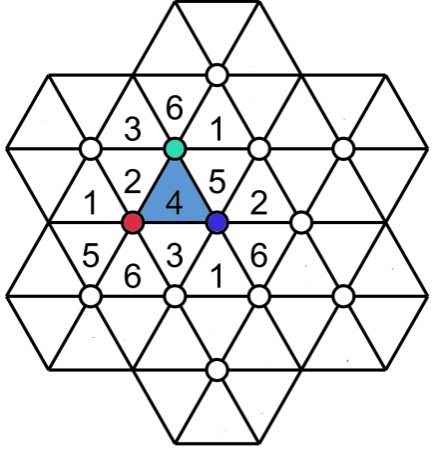
In this figure, the numbers for three hexagons with centre green, red and blue, are placed. The blue triangle with number 4 belongs to the three hexagons.
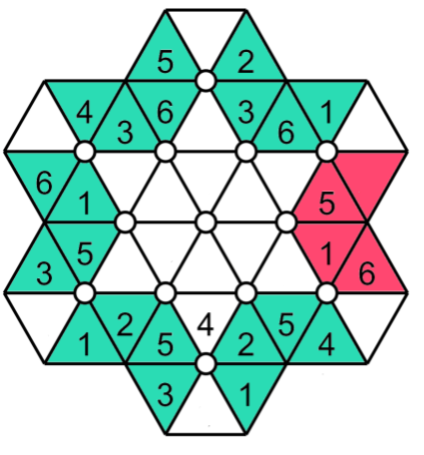
The partial hexagons along the border of the grid (each one having only 4 triangles) must have different number from 1 to 6 in the four triangles.
In this figure each partial hexagon is represented with green and red triangles. Notice that the partial hexagon in red does not respect the rule because two triangles has the same number 1.
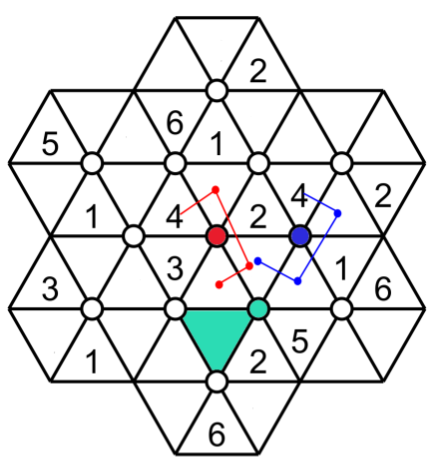
Number 4 must go in the green triangle for the green hexagon because some triangles of the green hexagon overlap with some triangles of the red and blue hexagons. And these two hexagons have already a 4. So the green triangle is the only empty triangle not overlapping with the red and blue hexagon.
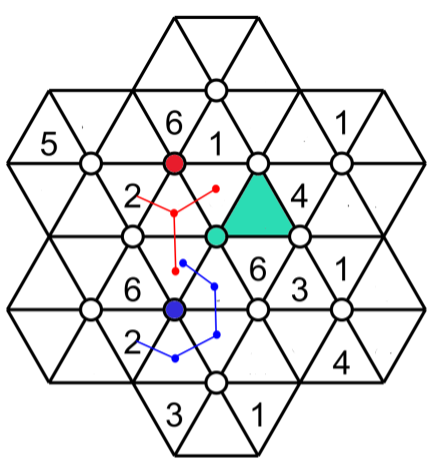
Use the same principle here. The number 2 must go in the green triangle of the green hexagon because the red and blue hexagon has already the number 2 and the green triangle is the only one in the green hexagon that does not overlap with the triangles of the red and blue hexagons.
